

Encryption is the idea of locking away information so that only
a person with the key can unlock and read it.
The simplest example of a code is the alphabetic substitution cipher.
Assume you want to send the following message in secret to a friend:
| Meet me in Princes Park by the fountain at 9:00pm tonight. |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
| a b c d e f g h i j k l m n o p q r s t u v w x y z |
| 0 1 2 3 4 5 6 7 8 9 _ ( ) + = - : ; " , . ? / $ |
| # ! @ * [ ] { } |
| v + # r - j 8 A K Q z T 2 , D u N Y m L d = ! X i } |
| ( t P s f B w n I 5 [ F l e 3 y V g ] q S 9 @ c J |
| ? h 7 0 o . k R ) 1 $ : O { 6 M p H U C Z x b * " |
| / ; a G 4 W E _ |
| 2ff]:FB:Il:urIlcBg:u(rk:tc:]nf:BeqF](Il:(]:1U??3F:]e{Iwn]b |
To send secret messages to a friend you give them the 86 character scrambled alphabet. Then sometime later, when you want to send a message, you use that alphabet as the code to create an encrypted version of the message. You can give the message to a messenger who will not be able to read it, and yet when it is delivered, your friend can read it; they can also send a secret reply using the same method.
How good is this method? There are 86! different codes. By this measure you are not going to find the answer by sequentially trying different codes. It looks perfect.
But the real answer is the code is not good. If your encrypted text falls into unfriendly hands, say the police, then it won't take them long to break your code. By just looking at the message, unless they are stupid, they will figure out that `:' is the character that represents blank. Other character equivalents will soon follow.
In World War II, the Germans used a machine for encryption called the Enigma machine. It was based on a character substitution cipher, but they complicated the process somewhat to make the code more secure. The Enigma changed the symbol substitution code every character.
The Enigma machine worked using a series of mechanical alphabetic `rotors'. Each rotor contained a random (but fixed) ordering of the symbol alphabet. The rotors were connected electrically so that if one put a voltage on an `a' it came encrypted as the voltage from position `M'. So each rotor did a single substitution cipher. The second rotor encrypted the output of the first rotor feeding it into the third rotor and so on. The final rotor would output this symbol on paper tape or transmit it. Then all the rotors would move, although the symbols sequence on each rotor would stay the same, this would cause a new cipher to be created for the next character, this would continue, creating a new cipher for each character of message. Before the start of every message the machine was reset to a standard position.
Messages encrypted by an Enigma machine are harder to break than a simple substitution code. Since each character in the message is encrypted with a new code one can not use any of the traditional statistical means for breaking the code. Because only the starting place changed from day to day and because the character sequence on the rotors never changed (it was too difficult mechanically to update all the Enigma machines), the allies with the help of the Polish underground did eventually read German messages.
If a new set of cipher wheels, a new machine, was used for each message then breaking the code while theoretically possible would practically become impossible because not enough data would be received to satisfy the equations. This approach is easy to do on a modern computer. Just make sure you have six or more rotors to keep the difficulty high. This is a fun practical project to do if you want to learn about encryption.
In 1917, a young engineer working for the American Telephone and Telegraph company in New York invented a simple effective cipher for the telegraph. In those days characters were typed on an electric typewriter that punched a `code' into paper tape. These tapes were then used to transmit the message. What Vernam did was use an extra punched paper tape reader at each end of the telegraph line. The extra paper tape reader had a loop of random characters on it. As the message was read to be transmitted, the tape reader would also read the next random character off the extra paper tape reader. A small electronic circuit would exclusive-or the bit pattern of the random character and the character of the message, this produced a random character to send out on the telegraph line. At the receiving end an identical copy of the random character loop was read by another paper tape reader. As data came in from the telegraph line it was exclusive-ored with the same random character that was used at the other end. This decodes the message and an electronic typewriter would print it.
This Vernam cipher uses the property of exclusive-or that:
| A XOR B = C |
| A XOR C = B |
| B XOR C = A |
The XOR bit function has an interesting information theoretic property as well.
If a series of bits, X has entropy, HX,
and another independent series of bits, Y has entropy, HY,
then the entropy of the exclusive or
is 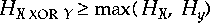 .
This means that combining independent sources of different entropies with
exclusive-or allows one to mask one source with noise from another source.
This is what the Vernam cipher does, it completely masks the
information in the message by saturating it with noise from the random
character loop.
This is also true of more than one source of independent bits, combine
twenty streams of bits by exclusive-oring them together, the entropy
of the combined source will approach noise.
This is like listening to twenty radio stations all at the same volume;
the result maximizes the noise, or you might say that you were getting
too much information all at once.
.
This means that combining independent sources of different entropies with
exclusive-or allows one to mask one source with noise from another source.
This is what the Vernam cipher does, it completely masks the
information in the message by saturating it with noise from the random
character loop.
This is also true of more than one source of independent bits, combine
twenty streams of bits by exclusive-oring them together, the entropy
of the combined source will approach noise.
This is like listening to twenty radio stations all at the same volume;
the result maximizes the noise, or you might say that you were getting
too much information all at once.
How secure is the Vernam cipher? It really depends on two things: the unpredictability of the cipher keys; and the length of the loop. If the cipher characters are not random then one can predict the series and decode the message. If the cipher characters are really random and the length of the loop is longer than the message, then the message without the key is impossible to decode. That is, the result is a perfect cipher.
If the loop repeats or is used again then the code may be broken. Because of this restriction, the most common name for a Vernam cipher used in this way is `the one-time pad'. One time pads provide perfect codes. However they depend on a key as long as the message. This is a bit of a problem if one is going to transmit many secret messages.
However if one had a good pseudo-random number generator in which the sequence is predictable only after doing some computationally infeasible task then one could use the seed as the key and easily produce encrypted messages. Many computer scientists doubt that a completely satisfactory, fast pseudo-random number generator can be built for this purpose. But it seems every year an article appears that moves us closer toward achieving that practical result.
From an information theoretic point of view the one-time pad,
produces noise, that is maximum entropy.
This despite one of its components, the message, has low entropy.
So good encrypted messages are a good source of random numbers,
but they rely on a good unpredictable source to produce them.