For a pseudo-random number generator to produce practical randomness
the next random should not be predictable from prior randoms,
the distribution of numbers should be uniform, and the sequence
should be sufficiently long that in practical terms it is inexhaustible.
The real world and the mathematical world are not the same.
The universe is probably finite.
It has a limited amount of matter and energy.
Recent estimates put the start of universe (the big bang)
at some where between 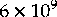 and
and 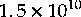 years ago.
There are about 3,155,7600 seconds per year.
This gives a generous estimate of
years ago.
There are about 3,155,7600 seconds per year.
This gives a generous estimate of 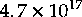 seconds
since the big bang.
A nano-second is the time it takes light to go about a foot.
In nano-seconds this is
seconds
since the big bang.
A nano-second is the time it takes light to go about a foot.
In nano-seconds this is 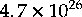 .
Gates on current machines operate in the nano-second range.
Multiplying by our magic number, 3.32, we can get an estimate
of this size as a binary number: 287, or 87 bits.
So 290, or 90 bits, is number that provides a practical limit
to counting.
If we started at the big bang and counted advancing one every nano-second
we would still be less than a eighth of the way to getting to 290.
So if we can produce pseudo-random numbers with a period of 290,
which have all the other distributional and unpredictable qualities
we want then we have effectively produced real random sequences, at
least for mortals in this world.
.
Gates on current machines operate in the nano-second range.
Multiplying by our magic number, 3.32, we can get an estimate
of this size as a binary number: 287, or 87 bits.
So 290, or 90 bits, is number that provides a practical limit
to counting.
If we started at the big bang and counted advancing one every nano-second
we would still be less than a eighth of the way to getting to 290.
So if we can produce pseudo-random numbers with a period of 290,
which have all the other distributional and unpredictable qualities
we want then we have effectively produced real random sequences, at
least for mortals in this world.
If the starting conditions for a pseudo-random number generation
are finite, then how many sequences of numbers can be produced by
the generator?
Clearly there is only one for each possible seed.
If there are 64-bits of seed, then there are only 264 different
random sequences.
If the period of the random number generator is 230 and it
doesn't repeat a number then there are 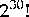 different possible
sequences.
This is a number much larger than the number of possible sequences
that could be generated from a pseudo-random generator;
however if you can't tell which one of the 264 seeds is being used
then the next number in the sequence may still be unpredictable.
Searching for the right seed, given just the output, is a difficult task.
The more difficult it can be made, then the better the random number generator.
different possible
sequences.
This is a number much larger than the number of possible sequences
that could be generated from a pseudo-random generator;
however if you can't tell which one of the 264 seeds is being used
then the next number in the sequence may still be unpredictable.
Searching for the right seed, given just the output, is a difficult task.
The more difficult it can be made, then the better the random number generator.
Where should one get a seed for a pseudo-random generator?
Picking a `random' number generated from the `real' world
is a good idea. This should make each possible seed equi-probable.
One source of `randomness' often used in computers is to pick a
state of the system that `unpredictable'.
For example if the system has a fast clock that counts to 50,000
every second and one assumes that the moment within a second that
one reads the clock is unpredictable, it will yield about 16 bits
worth of random seed.
If you assume which minute is unpredictable (a dubious assumption)
this gives another 6 bits worth of information.
If the operating system keeps track of processes by incrementing
a number for each new process and you also assume that the process
number is unpredictable then one might get 8 more random bits.
This is still far short of the 64 bits one needs to get a good
random sequence.
It would be useful if computers would generate good randoms based on
physical events when they weren't doing anything else; then one could
have a good new seed any time one wanted.
However lacking a good source of random numbers within a machine
we will look later in these notes at methods of expanding the randoms
we can get.
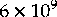 and
and 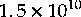 years ago.
There are about 3,155,7600 seconds per year.
This gives a generous estimate of
years ago.
There are about 3,155,7600 seconds per year.
This gives a generous estimate of 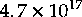 seconds
since the big bang.
A nano-second is the time it takes light to go about a foot.
In nano-seconds this is
seconds
since the big bang.
A nano-second is the time it takes light to go about a foot.
In nano-seconds this is 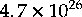 .
Gates on current machines operate in the nano-second range.
Multiplying by our magic number, 3.32, we can get an estimate
of this size as a binary number: 287, or 87 bits.
So 290, or 90 bits, is number that provides a practical limit
to counting.
If we started at the big bang and counted advancing one every nano-second
we would still be less than a eighth of the way to getting to 290.
So if we can produce pseudo-random numbers with a period of 290,
which have all the other distributional and unpredictable qualities
we want then we have effectively produced real random sequences, at
least for mortals in this world.
.
Gates on current machines operate in the nano-second range.
Multiplying by our magic number, 3.32, we can get an estimate
of this size as a binary number: 287, or 87 bits.
So 290, or 90 bits, is number that provides a practical limit
to counting.
If we started at the big bang and counted advancing one every nano-second
we would still be less than a eighth of the way to getting to 290.
So if we can produce pseudo-random numbers with a period of 290,
which have all the other distributional and unpredictable qualities
we want then we have effectively produced real random sequences, at
least for mortals in this world.
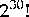 different possible
sequences.
This is a number much larger than the number of possible sequences
that could be generated from a pseudo-random generator;
however if you can't tell which one of the 264 seeds is being used
then the next number in the sequence may still be unpredictable.
Searching for the right seed, given just the output, is a difficult task.
The more difficult it can be made, then the better the random number generator.
different possible
sequences.
This is a number much larger than the number of possible sequences
that could be generated from a pseudo-random generator;
however if you can't tell which one of the 264 seeds is being used
then the next number in the sequence may still be unpredictable.
Searching for the right seed, given just the output, is a difficult task.
The more difficult it can be made, then the better the random number generator.