One can organize the hash table as a bin array of b pointers, where each pointer points to a list of records containing the information in the bin. The program uses the hash function on the key to pick the `bin', this bin is searched for the key.
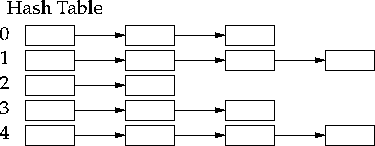
One can think of a hash table as an array of linked lists in which the head of each list is stored in an array. In the diagram below the first pointer to each chain is in the hash table, the remaining boxes are either one of two things. First the box can be a pair of pointers, one to the next member of on the bin list and the other to the data. Or it can be the desired record itself, which must have in it a next-field for pointing to the next record on the bin list. If the data only occurs once in the hash table then using the records themselves saves space. If a record can occurs more than once because different keys can access the same record then it will probably be better to have the bin list elements point at the data. This organization can be visualized as shown below.

In the hash table example above there are 5 bins, it has 11 keys recorded. The density or load factor is 2.2. There are no empty bins. Assume the bins are unordered. The average successful search will take 1.7 comparisons. The average unsuccessful search will take 2.2 comparisons. If the bins are ordered by some data property, like the key value, then the unsuccessful search can be reduced to 1.1 comparisons.
It doesn't take much extra work to keep bins in order. Records just need to be inserted in key order. So it is probably worth doing since it reduces the cost of building the data structure in the first place, and then reduces the all over cost by reducing the cost of unsuccessful searches.
In general if you choose the load factor to be moderate, there will be little unused space in the hash table then space can be saved by making the hash table contain the records instead of pointers. Thus the hash table becomes an array of records. Each record still needs to have a pointer to the next element in the bin to resolve hash clashes, and you must be able to determine if first record is empty or full. This will save about 4b bytes of storage, this can be significant space if b is a large number, but it will still always be a small percentage of the space used by the data structure.
This method, and its variants, are all called
direct chaining, it is easy to use and completely effective. Standard data structure textbooks give several other methods for organizing the hash table, these alternatives mostly compensate for bad hashing by filling in empty table locations. If you have a good hash algorithm, and there are three in this set of notes if used properly, then you don't need to worry about unexpected unused space; separate chaining gives you complete control of the time-space tradeoff.