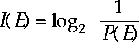
It is now time to take a deeper look at a bit, and how a bit represents information. The view we are going to take is from the perspective of the mathematician Claude Shannon. He tried to build a mathematical, or statistical, characterization of information. Information is an overused word; it means too many different things. Shannon restricted his theory to talking about communication channels and the signals that are communicated over them. Channels can be understood in a general sense, a program that takes data in and writes data out is a channel. A telephone line that connects me to someone else is a communications channel. And in some sense, each of us as individuals is a slow communications channel: we accept information and deliver it at some other time, like on the final exam. If the information comes out exactly as it went in then the channel is a good (or error-free) communications channel, otherwise it is called a noisy channel.
In the mathematical theory of information, that we are about to explore, information is concerned primarily with the form (the code) and constraints on what can be communicated on these information channels. This is a mathematical foundation for information engineering.
It is true that the human sense of information (e.g. I know you love me!) does not have much to do with symbols and channels, it is also true that fundamental communication constraints may have a great deal to do with the way we communicate among ourselves, including the semantic, psychological and linguistic aspects of human behavior.
The computer is a machine for manipulating symbols; at its heart is information represented as bits. This mini-survey of information theory should add depth to your understanding of what a bit means.
At the beginning of these class notes we characterized flipping a coin as the classic example of a source that gave a single bit of information.
The assumption made was that it was equally likely that a head or tail would occur. What if one flipped a biased coin, there are still two possible outcomes but they are not equally likely. If one knows the way the coin is biased, and one bets on that side; one will win more often than not. If one can talk someone else into believing that the coin is not biased they will give you even odds and one will randomly, but consistently, take their money. One knows something they don't know and the outcome of the coin toss is not yielding 1 bit of information but something less than one bit.
Let's construct an ideal coin, for our cheating gambler, it has a head on both sides. If he always bets on heads, he will always win. The coin flip now represents no information at all. Anyone who knows the coin can predict the result without flipping it. This coin flipped gives no information. And if the opponent examines it the gambler is likely to loose his life.
Let's make a weighted coin that can come out heads or tails, but it is
biased towards one or the other.
If the gambler always bets on heads, he will win in the long run.
There must be some function that measures the amount of information
(a number somewhere between zero and one bit) that shows how much
information a biased coin toss will give, knowing the probability of heads.
For event, $E$, whose probability of occurrence, $P(E)$, is known,
or can be estimated, then we can define $I(E)$ the information returned
by the occurrence of $E$, as
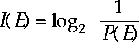
Assume that a series of coin tosses are made. This gives a series of symbols representing the outcomes which are statistically independent. Individually each symbol can be either a head or a tail. Can the information content of this source be computed?
Define $H(S)$ to be the entropy or information measure of the source. This is the sum of the probability of a symbol times the information that symbol provides. This is reasonable since the symbol will occur with its probability and add that much information to the output of the source. The sum of the probabilities should be one for any single source, since for any source some information must be forthcoming.
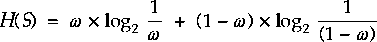
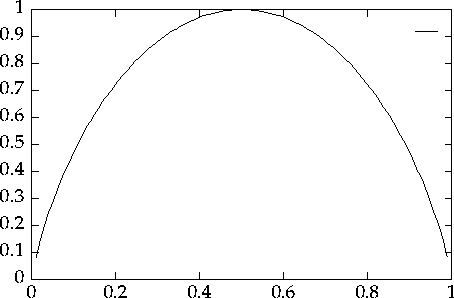
| Entropy (or Information) from a Boolean Source |
| The probability, $omega$, of getting a l is the horizonatal axis. |
| H(S) is represented in bits on the vertical axis. |
Now consider a source that instead of emitting just two symbols, emits sixteen different symbols, each equally likely. Again the information content of the source should be the sum of information for each of symbols times the probability of that symbol occurring. Thus for 16 equally likely symbols one gets: $sum from i=1 to 16 ~~ { 1 over 16 ~ times ~ log sub 2 ~ 1 over 1/16 }$, which simplifies to 4.0 bits. This answer is consistent with what we observed earlier, that it takes 4 bits to represent 16 equally likely symbols.
However the new formula lets us determine the information content of symbols that are not equally likely, so it covers biased symbols as well. For example the letters of the English alphabet are not all equally likely so the information content of each letter is not equal. Later we will compute the entropy of English in several different ways.
The highest entropy is always obtained when all the symbols are equally likely. If any one symbol is more (or less) likely than the others then the information content of the source will drop.
Note that bits in this information theory sense are a measure of information. When we write binary digits they may or may not contain that much information. The binary digits we write should really be called
binits for binary digits, rather than bits, which is a measure of information. But `bits' is the word that is commonly used for both information and binary digits. Don't confuse the amount of information needed to represent something with the number of binary digits that are written down. In a biased coin toss the information returned can be anything from 0 to 1 bit, but a coin toss result, head or tail, can always be represented as 1 binit.Note the number of information bits is always less than or equal to the number of binits. It is impossible to represent more than $b$ bits of information in less than than $roman ceil ( b )$ binits. So the ceiling of the information content gives you an lower bound on the number of binits you need to store something.
Let's play with this idea a little bit (just to pun a bit). How much information is represented by a deck of 52 playing cards. How many different ways can a deck of 52 cards be arranged? 52! How big is 52 factorial? According to my math tables it is: $8.0658 \(mu 10 sup 67$, or a large number. How many bits will it take to represent this number? $log sub 10 ~~ 8.0658 ~~ \(mu ~~ 10 sup 67$ is 67.90665 multiply that by our magic number 3.3219, and one gets 225.5791 bits, or about 226 bits of information in a deck of cards.
Well that is interesting! But so what? If one uses 6 binits to represent each card then 52 cards will occupy 312 binits. But the deck can store only 226 bits so 86 bits of information are wasted using this simple representation of a deck. Now, eleven bytes (88 bits) are probably not enough to worry about so perhaps storing 6 bits per card is a reasonable representation. But if you were pressed for space this simple calculation tells you there is a more efficient representation. It doesn't tell you what that representation is.
In this way the information content provides us with an efficiency measure for ways of representing information. This gives us a sense of how well we are doing.
Here is another card related question. How much information is in a cut and shuffle of a deck of cards? This is a much harder question. Let's look at a case we might be able to figure out. First assume the cut can happen anywhere in the deck including none on the top and none on the bottom. The deck can then be represented as a series of zeros followed by a series of ones. Where the total of zeros and ones must be 52. The zeros represent those that were on the bottom of the cut and the ones represent the ones that were on the top of the cut, so each card is either on the bottom or the top. Then these two sets of zeros and ones are interleaved in the shuffle. They create all kinds of bit string of zeros and ones. All the possible different cut-and-shuffles can be represented by a bit string of 52 zeros and ones. If each one of those possibilities is equally likely then there are 52 bits in a ideal cut-and-shuffle.
There are less than 52 bits worth of information because some bit strings are sure to be more likely than some of the others. Thus 52 is a greatest case estimate of the information content. But 52 is much less than 226, so most of the information in a deck of cards is still there after a cut and shuffle. In the best case after 5 cut-and-shuffles enough information would have been injected into the deck to completely randomize it. But to really randomize a deck you probably need to shuffle it at least once and possible twice more. So 6 to 7 cut-and-shuffles is probably the right amount if you want to play a fair card game. Now that's a practical result of information theory.
We noticed earlier that the letter in English are not equally likely. So let's turn to language and think about communication sources that output characters. Jonathan Swift in
Gulliver's Travels describes a research establishment in which hundreds of monkeys are seated typing random sentences. The manager of the enterprise is sorting the output by quality. He points out that eventually all knowledge will come his way, and research is really only a matter of sorting.If one treats the monkeys as an information source, how much `information' or entropy does the source produce? Assume that English can be written with 27 symbols, the 26 letters and a space; the information content of this source would be $log sub 2 ~~ 27 ~~=~~ 4.75$ bits/symbol. One might call this the zeroth approximation to English. It would yield string of characters like:

| Probability of English Letters |

Output of a first approximation of English might look like this:

Assume we know the probabilities of pairs of alphabetic symbols in English. Given any letter a table of probability for the following letter can be constructed. Now the monkeys get taught that after a given symbol the next symbol should have the appropriate probabilities. These probabilities came from [Pratt 1942] as used in [Abramson 1968]. These examples of approximations of English and other languages also came from [Abramson 1968]
Assume the monkeys use the two preceding letters and choose the next one with the right probability, how close is this to English? This then would be a third approximation. Shannon estimated the entropy of this third approximation as 3.1 bits per symbol.
This comes pretty close to program documentation turned in by 07.105 students. So the approximation to English must be pretty good.
Doing a fourth approximation along these lines requires processing much text and estimating the probability tables. These will be big: $27 sup 3$ is about 20,000 probabilities. Also the cost of monkeys smart enough to type with these probabilities is considerable -- so it may not be economically feasible to do the experiment. It could be done, of course, but I couldn't find the tables anywhere. Maybe you would like to generate the tables and do a fourth approximation. When you get the tables you should be able to work out the entropy of the source; it will probably be around 2.9 bits/symbol.
Abramson gives successive approximations to several other languages,
using statistical tables for those languages.
Here is the data he gives.
Can you identify the languages?
Language A.



Note that the estimate of the entropy of an English source gets lower as more probabilistic internal structure is accounted for in the output. With an entropy of 3.1 bits per symbol when the third approximation to English is considered one expects that English text could be compressed considerably. Usually there are 8-bits per alphabetic symbol, using ASCII text, one would expect that compression programs should be able to reduce English text by about 60%. The real entropy for English is indeed somewhat smaller so the compression should be able to do somewhat better than that. If you use a standard compression program like `compress' it usually compresses English text by about 60%, so these estimates are probably pretty close to accurate.
The entropy of a source gives us a measure for what the minimum storage should be for elements produced by that source. Random elements that are equally likely are the most uncompressible; the more structure and redundancy the source has; the more predicatable it becomes; and the more compressible it is.
Representing information as bits, or numbers, is a fundamental method in computer processing. I hope these class notes have given you some insight into the methods and dangers that lurk in the coding of standard items like truth values, numbers, and characters.
In the next set of class notes I will apply these bit coding
methods and show how a computer and programs can all be represented
by bits.
If bits can be implemented easily in electronics then this representation
will allow one to create a physical machine that will `compute' according
to instructions of its programmer.